国語 赤い繭(高校3年生で実施)
安部公房『赤い繭』について、「おれ」(権力を持たざる者)と「棍棒を持った彼」(権力を持つ者)との関係性、物語全体の構成、物語の悲劇的な結末、の3つの観点から読解を行った生徒たちが集まって、「おれ」が「赤い繭」になったことの意味を解釈します。「人間疎外」というテーマに迫ります。
ジグソー課題
「おれ」が「赤い繭」になることについて、どのような解釈が可能か。
エキスパート
エキスパートA:中心人物・重要人物(「おれ」と「棍棒を持った彼」との関係性)
エキスパートB:場面分け(物語全体の構成)
エキスパートC:表現の意味を考える(物語の悲劇的な結末)
エキスパートB:場面分け(物語全体の構成)
エキスパートC:表現の意味を考える(物語の悲劇的な結末)
期待する解答の要素
「人間疎外」という意味に類した解釈が出来ることが望ましい。
しかし、現代社会で人間が苦悩をしている状況が読み取れれば十分な評価としたい。
しかし、現代社会で人間が苦悩をしている状況が読み取れれば十分な評価としたい。
ポイント
生徒たちにとって抽象的で何が暗示されているのかが見えにくい小説を、「人物」、「場面」、「表現」に注目させる問いを設けることで読み取りを助け、結果的に生徒たちは授業者の想定を超える読みに到達しました。今回授業前・授業後に尋ねているのは「『赤い繭』を読んで最も強く自分に語りかけてきたことは?」というオープンな聞き方の質問ですが、ジグソー課題はそれよりもクローズドな問いにすることで、ねらいに応じた探究の深まりを引き出しています。もちろん授業前にジグソー課題と同じ問いを尋ねてみて、この点に関する生徒たちの理解の深まりを見えるようにするデザインも可能でしょう。
国語 永訣の朝(高校2年生で実施)
「永訣の朝」というテクストに表現された宮沢賢治の思いとはどのようなもので、どこへ向かっていくものだったのだろうか。雪を中心とした情景描写 の比較、作品の最後における作者の心情、表記表現上の特色という3つの視点をもとに、賢治の祈りに迫るような深い読解に挑みます。
ジグソー課題
宮沢賢治作「永訣の朝」からどのようなことが読み取れますか。
エキスパート
エキスパートA:「あめゆじゆ」などプラスのイメージの語、「みぞれ」などマイナスのイメージの語について
エキスパートB:作品の最後の部分に込められた「わたくし」の心情について
エキスパートC:「いもうと」の発話の反復やローマ字など表現上の特色について
エキスパートB:作品の最後の部分に込められた「わたくし」の心情について
エキスパートC:「いもうと」の発話の反復やローマ字など表現上の特色について
期待する解答の要素
作者が死にゆく「いもうと」のことを悲しみ嘆いていること
・しかしその作者に逆に「いもうと」が配慮を示したこと
・それにより作者は救われ、希望をも感じて、「いもうと」のけなげさがある種、世界の普遍的な尊く美しいものへと昇華されてほしいと祈るようになる。
ただし、上記に言及するだけでなく、さらに多様でユニークな気づき、一層深い読解に到達して欲しい。
・しかしその作者に逆に「いもうと」が配慮を示したこと
・それにより作者は救われ、希望をも感じて、「いもうと」のけなげさがある種、世界の普遍的な尊く美しいものへと昇華されてほしいと祈るようになる。
ただし、上記に言及するだけでなく、さらに多様でユニークな気づき、一層深い読解に到達して欲しい。
ポイント
本作品について一度学んだことのある生徒たちに対し、さらに深く多様な読みに到達してほしいとのねらいでデザインされた授業です。この授業の最初の段階では、期待する解答の要素のうち、作者の嘆きといもうとの配慮については気づいている生徒もいたものの、その先の作者の祈りにまで言及する生徒はいませんでした。それが授業の最後の記述では、「最初、私はこの作品を…悲しいものだという風に解釈していました。しかし、詩の中にちりばめられた様々な賢治とトシ子の思いを感じ、この作品は決して悲しいだけの、辛いだけの詩ではないと思いました」といったような回答がみられ、多くの生徒が授業者の期待を超えていくような多様で深い読みに到達しました。
英語 ing(高校2年生で実施)
生徒が混同しがちな「ing」の使い分けを意識するために、「進行形」、「動名詞」、「現在分詞」をそれぞれ復習して専門家となった生徒たちが集まって、1つのイラストに描かれた状況を3つの「ing」を用いて表現し分ける活動を行います。
ジグソー課題
1つのイラストに描かれた状況をingを用いて英語で表現してみる
エキスパート
エキスパートA:進行形の復習
エキスパートB:動名詞の復習
エキスパートC:現在分詞の復習
エキスパートB:動名詞の復習
エキスパートC:現在分詞の復習
期待する解答の要素
進行形、動名詞、現在分詞について、それぞれの使い方を発表できる。また、絵を見て、その状況を進行形、動名詞、現在分詞を使い分けて文を作ることができる。
ポイント
もとは、3つの文法事項の学習を一通り終えた段階で計画された授業です。1つのイラストに描かれた状況をingを用いて3通りに英語で表現してみる活動を行うことをとおして、授業前に1種類だけ書けた生徒は3種類の英文を書けるところに、授業前に3種類の文が書けた生徒も、文法的な違いを明確に意識して書けるところへ、それぞれ理解が深まりました。授業を受けた生徒からは「私たちこれまで英語どうやって勉強してたんだろう」という声も出てきて、文法の学習そのものを見直す機会にもなっていることがうかがわれました。
英語 Mermaid Balloon(高校1年生で実施)
それぞれ少しずつ情報が欠落した3つの英文を読んだ生徒たちが、自分たちの英文から得た情報を出し合い、絵を並べ替える活動に取り組む事を通して、ストーリーの全体像を組み立てていきます。
ジグソー課題
絵課題(絵を並べかえる等の課題)への取り組みを通して、読んだ英文の内容を報告しあい、ストーリー全体を把握する。
エキスパート
エキスパートA:ディジーの父親が亡くなっているという情報が欠落した英文
エキスパートB:ディジーが風船に手紙をつけて送ったという情報が欠落した英文
エキスパートC:誰が、どうして風船に手紙をつけて送ったという情報が欠落した英文
エキスパートB:ディジーが風船に手紙をつけて送ったという情報が欠落した英文
エキスパートC:誰が、どうして風船に手紙をつけて送ったという情報が欠落した英文
期待する解答の要素
・正しい順序で絵を並べ替えて、ストーリー全体を把握できること。
・場面ごとに正しい英語の説明文を選べること。
幼くて父親の死の意味が理解できないディジーが、父の誕生日に風船につけて飛ばした手紙に、返事とプレゼントが届けられたストーリー。
・場面ごとに正しい英語の説明文を選べること。
幼くて父親の死の意味が理解できないディジーが、父の誕生日に風船につけて飛ばした手紙に、返事とプレゼントが届けられたストーリー。
ポイント
英語が得意でない生徒を対象に計画された授業です。生徒たちは自分が読んだ英文にあてはまる絵を選択したり、絵を並び替えたりするための根拠を求めて、普段ならあきらめてしまう英文を一生懸命和訳するなど主体的に取組ました。発展課題として各絵に英語でキャプションをつけてみる課題が提示されましたが、どのグループも短時間で候補のキャプションを適切な絵にあてはめており、活動をとおして英語と場面を結びつけられるようになったことがうかがわれました。
理科 葉が緑色に見えるのはなぜか(高校3年生で実施)
葉が緑色に見えるのはなぜか。同化の単元の導入として、「色はどうしてみえるのか」、「葉緑体と光吸収スペクトル」、「エンゲルマンの好気性細菌を使った光合成の実験」という3つの情報を組み合わせてこの問いに答えを出します。
ジグソー課題
葉が緑色に見えるのはなぜか
エキスパート
エキスパートA:色はどうして見えるのか
エキスパートB:葉緑体と光吸収スペクトル
エキスパートC:エンゲルマンによる好気性細菌を使った光合成の実験
エキスパートB:葉緑体と光吸収スペクトル
エキスパートC:エンゲルマンによる好気性細菌を使った光合成の実験
期待する解答の要素
光合成に使わない緑色の波長を跳ね返しているため、私たちの目には葉が緑色に見える。
ポイント
身近な現象の仕組の解釈をとおして、既習事項である光のスペクトルや視覚に関する知識と、これから学ぶ同化の単元を結び付け、イメージを広げました。グループによっては「光合成ってそもそも何だっけ」というように、資料にない情報を思い出しながら対話を進め、結果的に本時で理解を深めたい知識の土台を洗い直すような対話が生まれました。この単元で教えるべき事項をバランスよく各エキスパートに配分した、というタイプの資料のつくりではありませんが、各資料が生徒の既有知識を引き出す手がかりとして有効に機能した例といえます。
数学 ベクトル(高校2年生で実施)
「ベクトルの実数倍、並行および3点が一直線上にある条件」、「ベクトルの和、分解、一次結合」、「ベクトルの差、内分点を表すベクトル」という3つの情報を組み合わせて活用し、「平行四辺形OABCにかかわる3点O、D、Eが一直線上にあることをベクトルを用いて示す」という課題に取り組む事を通して、ベクトルで考えることのイメージをつかみます。
ジグソー課題
平行四辺形OABC の対角線AC の1:2に内分する点をD、辺AB の中点をE とする。
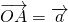 、
、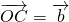 としたとき,次の問いに答えよ。
としたとき,次の問いに答えよ。
(1)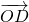 、
、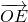 を 2つのベクトル
を 2つのベクトル 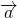 、
、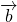 で表せ。
で表せ。
(2) 3 点O、D、E は一直線上にあることを示せ。
(1)
(2) 3 点O、D、E は一直線上にあることを示せ。
エキスパート
エキスパートA:ベクトルの実数倍、平行および3点が一直線上にある条件
エキスパートB:ベクトルの和、分解、一次結合
エキスパートC:ベクトルの差、内分点を表すベクトル
エキスパートB:ベクトルの和、分解、一次結合
エキスパートC:ベクトルの差、内分点を表すベクトル
期待する解答の要素
・どんなベクトルも、2つのベクトルで表せる。
・3点が一直線上にあることを自分でも証明できる。
・3点が一直線上にあることを自分でも証明できる。
ポイント
授業の構造として、次に紹介する「三角関数」の授業では3つのエキスパートは対等・同質な内容の並列となっていますが、こちらは並列でないエキスパートを組み合わせて答えを導く授業の構造になっています。こうした構造の場合、結果として3つの資料の関連性がより深まり知識が構造化されるように授業をデザインすればよい、と授業者は語っています。ただし、各エキスパートの内容としては異質な3つのものを盛り込みつつも、プリントのつくりを同じ構造(「使うべき知識」「その知識をどう使うかの例」「まとめ」)にした工夫が、生徒たちの活動の助けになりました。生徒たちの多くが、ベクトルは「文字式」のように「平行四辺形に」組み合わせることで、「どんなベクトルも」表せる便利なものであることを実感できる授業になりました。
数学 三角関数(高校2年生で実施)
関数グラフソフトGRAPESを使った授業です。三角関数グラフの 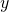 軸方向の拡大、
軸方向の拡大、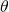 軸方向の拡大、
軸方向の拡大、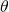 軸方向への平行移動の3つをそれぞれ数式と対応させて確認し、GRAPES上でグラフの変化の様子を確認します。その後、つかんだイメージを組み合わせて、複雑な式をグラフにする課題に取り組むことを通して
軸方向への平行移動の3つをそれぞれ数式と対応させて確認し、GRAPES上でグラフの変化の様子を確認します。その後、つかんだイメージを組み合わせて、複雑な式をグラフにする課題に取り組むことを通して 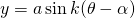 のグラフのイメージを描き、構造を理解させることがねらいです。
のグラフのイメージを描き、構造を理解させることがねらいです。
>「GRAPES」についてはこちら
>「GRAPES」についてはこちら
ジグソー課題
エキスパート
エキスパートA: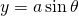 のグラフは
のグラフは 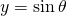 のグラフを
のグラフを 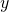 軸方向に
軸方向に 倍拡大したものである
倍拡大したものである
GRAPESを用いて の値を変化させたときのグラフの様子を調べるエキスパートB:
の値を変化させたときのグラフの様子を調べるエキスパートB: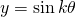 のグラフは
のグラフは 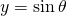 のグラフを
のグラフを 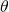 軸方向に
軸方向に 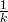 倍拡大したものである
倍拡大したものである
GRAPESを用いて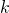 の値を変化させたときのグラフの様子を調べるエキスパートC:
の値を変化させたときのグラフの様子を調べるエキスパートC: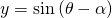 のグラフは
のグラフは 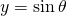 のグラフを
のグラフを 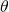 軸方向に
軸方向に 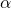 平行移動したものである
平行移動したものである
GRAPESを用いて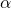 の値を変化させたときのグラフの様子を調べる
の値を変化させたときのグラフの様子を調べる
GRAPESを用いて
GRAPESを用いて
GRAPESを用いて
期待する解答の要素
資料
授業案1 教材1 振り返り1(実践例) 授業案2 教材2 振り返り2(実践例)
※GRAPESをダウンロードいただいた後、こちらのファイルをダウンロードしzipファイルを解凍すると、開くことができます。
ポイント
ICTを効果的に活用した授業例といえます。それぞれのエキスパートは既習内容の復習にあたり、生徒たちは、式の数値を変化させるとグラフがどう変化するか、実際に動かしながら観察しました。グラフが「伸びた」「動いた」といった直感的な理解を、数学的な言葉や表現を用いた説明におきかえながら、元のグラフが最終的にどのように変化するのかの説明づくりに組み入れていきました。ワークシートのつくりにも、生徒たちからいかに説明のことばを引き出すかについての授業者の工夫がみられます。穴埋めなどで思考の仕方を細かく誘導しすぎても、かえって生徒たちが自分たちの言葉で説明を組み立てることを難しくすることがあるという考察は、様々な授業の資料づくりに有効な指針となりそうです。
家庭 沖縄の食文化(高校2年生で実施)
ラード以外の油脂で「ちんすこう」のあのおいしさを作りだすことはできるか?バター、ラード、ショートニングの3つの油脂について学んだ生徒たちが集まって、それぞれの特性を比較しながら課題への答えを探ります。
ジグソー課題
ラード以外の油脂で「ちんすこう」のあのおいしさを作り出すことはできるか?
エキスパート
エキスパートA:バター(特徴、サブレとちんすこうの比較)
エキスパートB:ラード(特徴、沖縄の食文化、油脂の融点)
エキスパートC:ショートニング(特徴、油脂の役割、生地の可塑性)
エキスパートB:ラード(特徴、沖縄の食文化、油脂の融点)
エキスパートC:ショートニング(特徴、油脂の役割、生地の可塑性)
期待する解答の要素
製菓においては、油脂の選択が製品の出来栄えを左右する。調理時に、栄養、文化的背景、対象者など様々な視点で考え、根拠に基づいて材料を選択することが必要である。
ポイント
修学旅行の事前学習で、沖縄の食文化や、ちんすこうの歴史や原材料などについて学習した生徒たちに実施しています。ちんすこうがラードを用いて作られていることを知っている生徒たちだからこそ、この問いがうまく働きます。生徒たちは授業前に「できる」「できない」を十分な根拠なく予想していましたが、3種類の油脂の特徴と製菓の出来栄えに関わるポイントについて書かれたエキスパート資料を組み合わせることで、それぞれの油脂の特性を考慮した理由を挙げて解答できるようになりました。
美術 孔版について学ぼう(高校3年生で実施)
孔版の技法や制作方法、孔版の特徴、グラデーションの技法についてそれぞれ学んだ生徒たちが集まって、参考作品とできるだけ近い作品を制作します。孔版についての理解を深めて、自らのデザイン制作へとつなげていきます。
ジグソー課題
孔版を使った参考作品にできるだけ近い作品を制作しよう
エキスパート
エキスパートA:孔版の技法や制作方法について
エキスパートB:孔版の特徴(多色刷り、同じ版を繰り返し利用する)について
エキスパートC:グラデーションの技法について
エキスパートB:孔版の特徴(多色刷り、同じ版を繰り返し利用する)について
エキスパートC:グラデーションの技法について
期待する解答の要素
孔版の技法や特徴、その制作方法が理解できている。版画の製版の方法の特質や材料の活用を学べているか。絵の具の発色を活かし、グラデーションを表現できているか。
ポイント
最終的には自由な作品制作を行うことをねらいつつも、いきなりそこに向かうのではなく、まずは「参考作品にできるだけ近い作品を制作する」というジグソー課題を設けているのが工夫のポイントです。生徒たちは参考作品に使われている技法がどのようなもので、どんな絵の具の使い方、色づくりをしたのかを丁寧に鑑賞し、そのイメージ通り制作するために試行錯誤を重ねました。ここでの技法の理解の深まりが、結果的に自由制作の質の向上につながっていきます。技能系の教科の授業デザインをするうえで、こうした課題設定の仕方は参考になります。

